アインシュタイン宇宙からの帰還
Einstein, returning from space
|
(2018年11月22日) アインシュタインは目が覚めると自分が狭いエレベータのような室内にいることが分かりました。宇宙船に乗ってロケットで飛び出したときのショックで気絶していたようです。この部屋は宇宙船の中にあります。窓がありませんので外は見えません。部屋には明かりがあって部屋の中は良く見えます。じっと目をこらすと部屋には体重計とボールが一つ浮いています。気がつくと自分も浮いているのです。アインシュタインは無重力状態にある自分がどういう状況に置かれているのかを考えました。 ① エレベータの室内にいるがロープが切れて落下している アインシュタインは身震いしました。もしそうなら地上にすぐ叩きつけられてしまうからです。しかし、ふわっと浮いている時間が長いようなので安心しました。もし、ビルのエレベータにいるのなら500m落下しているとしても地上にたたきつけられるまで10秒しかありませんから。アインシュタインは暗算で落下時間を計算しました。 それでもビルが月面に建っているとするなら落下時間は500m落下するのに24秒ぐらいかかるなと思いました。月面での重力加速度は地球の表面での重力加速度の1/6です。しかし、ふわっと浮いている時間がまだまだ長いようなのでエレベータの落下ではないと確信しました。それではと別の状態を考えてみました。 ② 国際宇宙ステーションのように地球を周回している
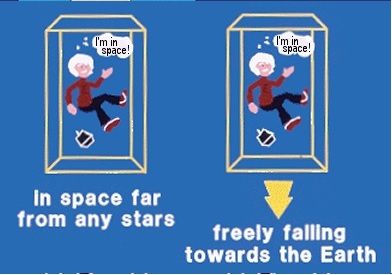
アインシュタインは国際宇宙ステーションの中で若田宇宙飛行士などが活動している様子を思い浮かべました。自分が浮いている状態はそっくりではありませんか。そうだ、地球から400㎞ほど離れて円軌道を周っているのかも知れない。 ③ 月までの楕円軌道を飛行している アインシュタインはアポロ計画の宇宙飛行士たちはサターン5型ロケットの上段ロケットが燃焼停止した後月まで片道3日間も楕円軌道を飛行していたことを思い浮かべました。そうだ、円軌道でなくても無重力状態にあるのは同じなのだと。月着陸船にはいつも2名が乗って月面着陸を果たしましたが、その間1名は司令船に残って月を周回していたのです。この司令船も無重力状態のまま2名が月面から戻ってくるのを待っていたのです。自分は今、月の周りを回っているのかもしれないとも思いました。 ④ 惑星フライバイをしている アインシュタインはパイオニアやボイジャーの惑星探査衛星が木星や土星の重力を利用してロケット燃料を使わずにさらに遠くの惑星探査を続けたことを思い出しました。惑星フライバイの途中では大きな惑星の重力により方向変更だけでなく加速もされています。外からこの宇宙船を観測すると大きな加速度飛行をしているのですが宇宙船内部では無重力状態であることに変わりはないのです。アインシュタインはさらに考えました。 ⑤ すべての星から遠く離れた何もない宇宙空間にいる すべての星から遠く離れた宇宙空間では重力も働きません。自分が動いているか止まっているかも分かりません。ただふわっと浮いていることは同じです。
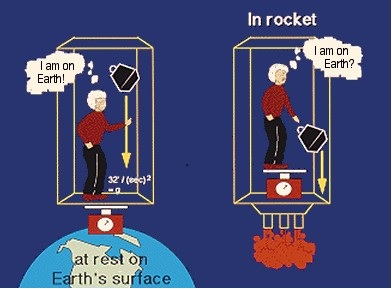
アインシュタインは自分の室内にあるのは体重計とボールだけですが、どのような道具や計測器があったとしても①の状態から⑤の状態までどれが自分の置かれた状態のなのかを決めることは出来ないと結論付けました。 アインシュタインはふと気がつくとボールも体重計も床にくっついているではありませんか。自分の身体も床に触っている。ボールを手に取って離してみるとボールはゆっくりと床に向かって動き出しました。体重計に乗ってみるとわずかに目盛りが動きます。アインシュタインは服を着た自分の体重が80キロ(80kg重)あるのを知っていました。このとき目盛りは1キロ(10ニュートン)も動いていなかったのです。この体重計はニュートン目盛りだったので、地表で普通に図ったなら800ニュートンを指すはずです。 アインシュタインはエレベータのような宇宙船がもはや次の⑥か⑦の状態にあると考えました。 ⑥ この宇宙船には姿勢制御用の小さなロケットが装備されていて、これが作動し小さな推力を発生している。 ⑦ 宇宙ステーションのように地球を周回していたが、高度が下がって薄い空気抵抗を受けている。 そして、この二つの状態が続けば、どちらであるかを区別することは出来ないのです。アインシュタインは再び居眠りをしてしまいました。 目を覚ますとボールも体重計も自分も床に張り付いています。ボールを手に取って放してみると今度は少し早く床に向かって動きます。体重計で自分を計ってみますと目盛りは130ニュートンを示しています。自分の体重は800ニュートンでしたから約1/6です。ここでアインシュタインは自分の置かれた状況を次のように考えました。 ⑧ エレベータは月面にいる(月面の重力加速度は地球表面の重力加速度の1/6) ⑨ 外部に取り付けられた比較的小さなエンジンが推力を発生している
⑩ エレベータが薄い大気に突入し、少し空気抵抗を受けている
アインシュタインは体重計はあるが他にどんな計器があったとしても3種の状況を区別することは出来ないことだと結論付けました。そして、再び居眠りに入りました。 しばらくすると、アインシュタインは自分が大きく床に押し付けられていることから目を覚ましました。床との間に体重計を挟みますと目盛りは800ニュートンをはるかに超えて2400ニュートンもあるではありませんか。 体重が3倍になっていることを知り、アインシュタインは3gの加速度を受けていることを知りました。このような状況になるのは二つ考えられます。スペース・シャトルが地上から飛び上がったとき、サターンVロケットで3人の宇宙飛行士が月に向かったときもエンジンが推力を出しているとき、乗組員達は3g前後の加速度を受けたことを思い出しました。また、これらの宇宙飛行士が地球に戻ってきたときも大気との摩擦を受けて真っ赤になって戻ってきたときも中の宇宙飛行士は3g程度の減速度を受けたことを思い出しました。 ⑪ エレベータを搭載したロケットが大きな推力を発生している ⑫ エレベータは大気に突入して減速している アインシュタインはやはりエレベータの内部にいるかぎり、どのような計測器を持ってきても⑪と⑫を区別する手段はないことを結論付けました。減速しているのか増速しているのかエレベータの中にいる限り加速度は区別できないのです。体重計は形状が車の座席のようになっているので耐えられました。 床から加わってくる大きな力に耐えた後、アインシュタインの体重計は800ニュートンで安定しました。このときアインシュタインは地球の表面に着陸したに違いないと思いましたが、まだ別の可能性があることに気がつきました。 ⑬ エレベータは地上に軟着陸していて静止している ⑭ エレベータはパラシュートを開いて定速で落下を続けている
長い時間が過ぎましたが漸く救助隊に外からエレベータのドアが開けられてアインシュタインは無事外に出ることが出来ました。アインシュタインの宇宙からの帰還は無事に終わりました。 体重計の指示値は換算して表示するだけで加速度計として見ることも可能でます。宇宙船が動いているか、静止しているかはエレベータの内部にいる人には分からないのです。アインシュタインはエレベータのような宇宙船の内部の状態について次のように二つにまとめました。 (A) 宇宙船が推力を出すこともなく、かつ外部から何も力を受けていないとき、内部の物はすべて浮遊する。すなわち、内部の物に何も力が働いていない。宇宙船が重力により動かされているときも同じであるので重力の有無を知ることは出来ない。 (B) 宇宙船が推力を発生したり何らかの力が外部から加わるとエレベータの内部のものはすべて力と逆向きの方向に加速度運動を始める。内部の物体が壁により運動を阻止されると壁から力を受ける。
(A) と(B)の関係から重力は力でないと結論できます。 (了) 戻る
|