正規分布

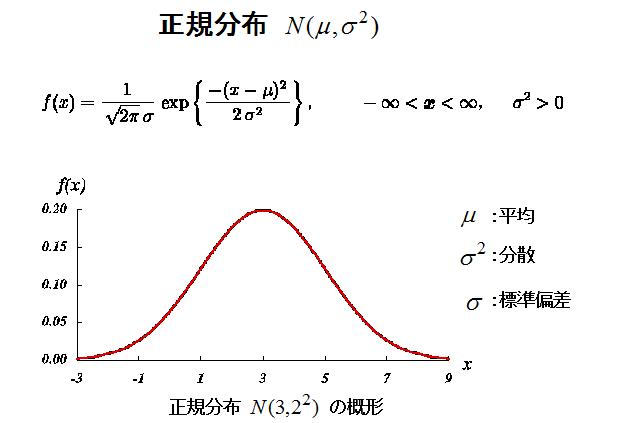
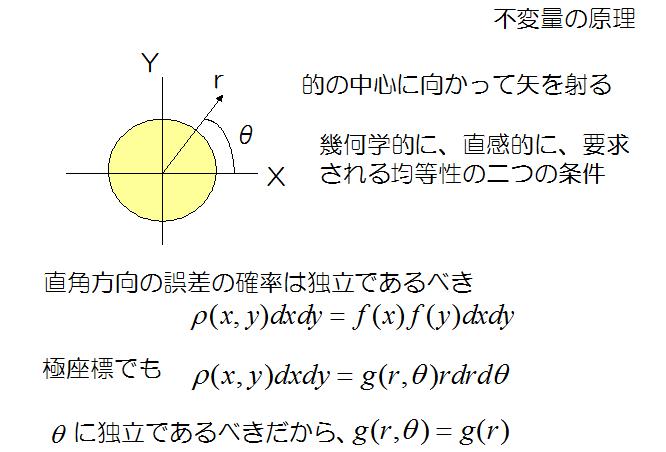
　身長の分布にしても体質量の分布にしても多くの分布が一つの釣鐘状を示すことが報告されています。
　的を射る競技には弓道、アーチェリー、射撃などがあります。競技者一人に注目すると何時も的の中心を狙っていても外れる方向が偏っていることが観察されます。これは人や道具の癖としてそれを知ることが練習の一つの成果でもあります。
　大勢の人の射撃を観察して結果（的に当たった場所）の統計を取り、2次元の図にしてみると、やはり中央を一つの山とする釣鐘型になっていることが多いのです。
　的を射たときの弾や矢の分布が2次元の正規分布に従うことは論理的推論の結果として示すことができます。論理的推論の概要は次のとおりです。
　この分布の形状を表す関数は直行座標軸の取り方で変わらない筈という条件に、極座標表示でも同じでなければならない筈であることを条件がある。つまりこの関数が満たさなければならない制約条件がある。そしてこれを満たす関数は2次元正規分布である。
　この2次元正規分布には一つパラメータが残り、それが散らばりの尺度を示す標準偏差σになります。
　このようなわけで、理由が判らなくて値がばらつくものは、正規分布を仮定することが妥当なのです。
　正規分布はガウスの誤差研究が有名でガウス分布とも呼ばれます。